RUMUS TRIGONOMETRI SMAN/SMA KELAS XI IPA

A. Penggunaan Rumus Sinus dan Cosinus Jumlah Dua Sudut, Selisih Dua Sudut, dan Sudut Ganda
1. Rumus Cosinus Jumlah dan Selisih Dua Sudut
Sebelum membahas rumus trigonometri cosinus untuk jumlah dan selisih dua sudut, perlu kamu ingat kembali dalam segitiga siku-siku ABC berlaku:

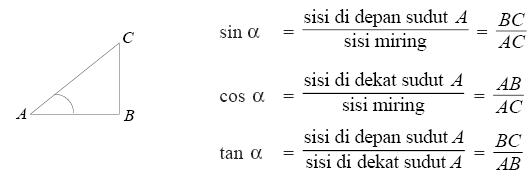
Selanjutnya, perhatikanlah gambar berikut.

Dari lingkaran yang berpusat di O(0, 0) dan berjari-jari 1 satuan misalnya,
∠ AOB = ∠ A
∠ BOC = ∠ B
maka ∠AOC = ∠ A + ∠ B

Dengan mengingat kembali tentang koordinat
Cartesius, maka:
a. koordinat titik A (1, 0)
b. koordinat titik B (cos A, sin A)
c. koordinat titik C {cos (A + B), sin (A + B)}
d. koordinat titik D {cos (–B), sin (–B)} atau (cos B, –sin B)

Rumus cosinus jumlah dua sudut:
cos (A + B) = cos A cos B – sin A sin B
Dengan cara yang sama, maka:
cos (A – B) = cos (A + (–B))
cos (A – B) = cos A cos (–B) – sin A sin (–B)
cos (A – B) = cos A cos B + sin A sin B
Rumus cosinus selisih dua sudut:
cos (A – B) = cos A cos B + sin A sin B

2. Rumus Sinus Jumlah dan Selisih Dua Sudut
Perhatikan rumus berikut ini.

Maka rumus sinus jumlah dua sudut: sin (A + B) = sin A cos B + cos A sin B
Dengan cara yang sama, maka:
sin (A – B) = sin {A + (–B)}
= sin A cos (–B) + cos A sin (–B)
= sin A cos B – cos A sin B
Rumus sinus selisih dua sudut: sin (A – B) = sin A cos B – cos A sin B

3. Rumus Tangen Jumlah dan Selisih Dua Sudut

4. Penggunaan Rumus Sinus, Cosinus, dan Tangen Sudut Ganda
Rumus untuk sin 2α
Anda telah mengetahui bahwa
sin (α + β) = sin α cos β + cos α sin β.
Untuk β = α, diperoleh
sin (α + α) = sin α cos α + cos α sin α
sin 2 α = 2 sin α cos α
Jadi, sin 2α = 2 sin α cos α

Rumus untuk cos 2α
Anda juga telah mempelajari bahwa

Rumus untuk tan 2α

Perkalian, Penjumlahan, serta Pengurangan Sinus dan Kosinus
Perkalian Sinus dan Kosinus
Kita telah mempelajari rumus-rumus jumlah dan selisih dua sudut dalam trigonometri, yaitu:

Penjumlahan dan Pengurangan Sinus
Rumus perkalian sinus dan kosinus dalam trigonometri di bagian C.1 dapat
ditulis dalam rumus berikut.

Identitas Trigonometri

Contoh Soal Trigonometri